Database computations on Z-sets (part 1)

Introduction

In a couple of blog posts we have introduced Z-sets as a mathematical representation for database tables and changes to database tables, and we have given a simple Java implementation of the basic Z-set operations. In this blog post we build a few additional methods for Z-sets which enable us to perform traditional database computations.

Recall that a Z-set is just a table where each row has an attached integer weight, which can be either positive or negative. We can then define operations of addition and negation for Z-sets, where the sum of two Z-sets contains all rows in either Z-set; the weight of a row in the result is the sum of the row's weights in both sets.

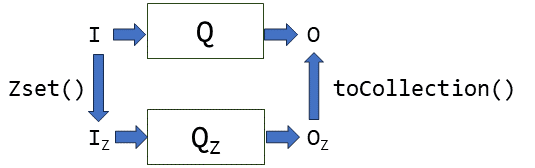
It helps to state exactly we want to achieve: our goal is the following: let's say we have a database table I and a query Q computing on table I to produce another table O.

The Java implementation has a method for converting a collection into a Z-set (the public ZSet(Collection<Data> data, WeightType<Weight> weightType), and another method toCollection that produces a collection from a ZSet.

We say that a computation QZ on Z-sets is correct if we have the relationship depicted in the following diagram:1

In words: if we execute query Q on input I we get the exact same result as if we convert I to a Z-set, compute using Q Z, and then convert the result to a table. This should be true for any input table I.

Notice that this rule does not say anything about what Q Z does when the input is a Z-set that does not represent a table. For these cases our function can do anything. But we will strategically chose implementations that give useful results even when the weights are negative.

Implementing database computations on Z-sets

All the code in this blog post is available in the Feldera repository in the org.dbsp.simulator Java namespace. In particular, all the following methods are in collections/ZSet.java.

Filtering (SQL WHERE)

For the first task we consider filtering, which is expressed in SQL as the WHERE clause in a query, e.g.: SELECT * FROM T WHERE T.COL > 10. Which rows of the input table are preserved in the result is decided by a predicate, which is a function that computes a Boolean value for each row of a table. In the previous example the predicate is T.COL > 10. In Java we will use the Predicate<T> interface to describe a predicate. The filtering function on Z-sets can be written as:

public class ZSet<Data, Weight> {
    // extending existing class

    public ZSet<Data, Weight> filter(Predicate<Data> keep) {
        Map<Data, Weight> result = new HashMap<>();
        for (Map.Entry<Data, Weight> entry: this.data.entrySet()) {
            Weight weight = entry.getValue();
            if (keep.test(entry.getKey()))
                result.put(entry.getKey(), weight);
        }
        return new ZSet<>(result, this.weightType);
    }
}

The filter function just applies the predicate to each entry in a Z-set; when the predicate is true the entry is added to the result, with its original weight (even if the weight is negative). This clearly gives the correct result when weights are all positive.

Transforming (SQL SELECT)

Let us consider a SQL query with a SELECT statement, without aggregation or grouping. The SELECT statement is followed by a list of expressions that are evaluated for each row of the source collection. The expressions can be simple column expressions SELECT T.COLUMN1 FROM T or they can be complex arithmetic expressions that involve multiple columns: SELECT T.COL1 + T.COL2 FROM T. We define a corresponding method for Z-sets called map: map is given by an arbitrary function, implementing the Java Function<T, R> interface.

public class ZSet<Data, Weight> {
    // extending existing class

    public <OData> ZSet<OData, Weight> map(Function<Data, OData> tupleTransform) {
        Map<OData, Weight> result = new HashMap<>();
        for (Map.Entry<Data, Weight> entry: this.data.entrySet()) {
            Weight weight = entry.getValue();
            OData out = tupleTransform.apply(entry.getKey());
            result.merge(out, weight, this::merger);
        }
        return new ZSet<>(result, this.weightType);
    }
}

Similar to the filter function, the map function is applied to each row and copies the weight of the source row to the destination row.

Let us notice two properties of map:

• applying map to a Z-set with positive weights will also produce a Z-set with positive weights.
• applying map to a Z-set representing a set (where all the weights are 1) may produce a Z-set where some weights are greater than 1. This is true in SQL as well, where SELECT 1 FROM T will produce a multiset with as many 1 values as there are rows in T.

Cartesian products

The Cartesian product of two sets builds all pairs of elements from two sets. In SQL this can be expressed in multiple ways. The simplest one is to just use multiple tables in the FROM clause: SELECT T.COL1, S.COL1 FROM T, S. This is also called a cross-join.

We implement a slight generalization of the Cartesian product for Z-sets, where the final result is obtained by applying a user-supplied function to each pair of rows. For this purpose we use the Java BiFunction<T, U, R> interface.

We call our Z-set operation multiply:

public class ZSet<Data, Weight> {
    // extending existing class

    public <OtherData, Result> ZSet<Result, Weight> multiply(
            ZSet<OtherData, Weight> other,
            BiFunction<Data, OtherData, Result> combiner) {
        ZSet<Result, Weight> result = new ZSet<>(this.weightType);
        for (Map.Entry<Data, Weight> entry: this.data.entrySet()) {
            for (Map.Entry<OtherData, Weight> otherEntry: other.data.entrySet()) {
                Result data = combiner.apply(entry.getKey(), otherEntry.getKey());
                Weight weight = this.weightType.multiply(entry.getValue(), otherEntry.getValue());
                result.append(data, weight);
            }
        }
        return result;
    }
}

There are two reasons this operation is called multiply:

• the number of rows in the result Z-set is the product of the number of rows in the multiplied Z-sets
• the weight of each row in the result Z-set is the multiplication of the weights of the corresponding rows in the source Z-sets

SQL UNION

The SQL UNION operation can be applied to two tables that have the same schema (same columns). It produces a table that contains all the rows that appear in either table. There are two forms of UNION in SQL: UNION ALL, which keeps duplicate records, and UNION, which strips away duplicates.

It turns out that we already have implemented the required operations on Z-sets: UNION ALL is the add method, while UNION is add followed by a call to distinct.

public class ZSet<Data, Weight> {
    // extending existing class

    public ZSet<Data, Weight> union(ZSet<Data, Weight> other) {
        return this.add(other).distinct();
    }

    public ZSet<Data, Weight> union_all(ZSet<Data, Weight> other) {
        return this.add(other);
    }
}

SQL EXCEPT

The SQL EXCEPT operation is only defined for two tables with the same schema, and where both are sets (no duplicates allowed). This operation keeps all rows from the first table which do not appear in the second table. We already have all the ingredients to build except:

public class ZSet<Data, Weight> {
    // extending existing class

    public ZSet<Data, Weight> union(ZSet<Data, Weight> other) {
        return this.add(other).distinct();
    }

    public ZSet<Data, Weight> union_all(ZSet<Data, Weight> other) {
        return this.add(other);
    }
}

We need to apply the operation distinct three times: once for each input, to make sure that the inputs are sets, and once for the output, to eliminate rows with negative weights. (If we know that an input is always a set, then the corresponding distinct can be omitted.)`

Aggregations

An aggregation function in SQL transforms a collection into a single value. The most common aggregation functions are COUNT, SUM, AVG, MIN, MAX. Each of these operations can be expressed as a loop that keeps updating an accumulator, with logic defined by the following pseudo-code:

accumulator = initialValue;
foreach (row in collection) {
   accumulator = update(accumulator, row)
}
return finalize(accumulator)

initialValue is the result produced when the collection is empty. The finalize step is used for computing aggregates like "average," which will use it to divide the sum of values by their count.

To compute on Z-sets we will generalize this scheme slightly to allow aggregating values with a weight. We define a helper class AggregateDescription which bundles three pieces of information:

public class AggregateDescription<Result, IntermediateResult, Data, Weight> {
    public final IntermediateResult initialValue;
    public final TriFunction<IntermediateResult, Data, Weight, IntermediateResult> fold;
    public final Function<IntermediateResult, Result> finalize;

    public AggregateDescription(IntermediateResult initialValue,
                                TriFunction<IntermediateResult, Data, Weight, IntermediateResult> update,
                                Function<IntermediateResult, Result> finalize) {
        this.initialValue = initialValue;
        this.update = update;
        this.finalize = finalize;
    }
}

Unfortunately Java does not have a TriFunction interface similar to BiFunction, so we had to define our own in a separate file. The definition is very simple:

@FunctionalInterface
public interface TriFunction<T, U, V, R> {
    R apply(T var1, U var2, V var3);
}

With these preparations the implementation of aggregate looks very much the pseudo-code above:

public class ZSet<Data, Weight> {
    // extending existing class

    public <Result, IntermediateResult> Result aggregate(
            AggregateDescription<Result, IntermediateResult, Data, Weight> aggregate) {
        IntermediateResult result = aggregate.initialValue;
        for (Map.Entry<Data, Weight> entry : this.data.entrySet()) {
            Weight weight = entry.getValue();
            result = aggregate.update.apply(result, entry.getKey(), weight);
        }
        return aggregate.finalize.apply(result);
    }
}

In a future installment we will talk about additional computations on Z-sets, such as GROUP-BY and JOIN.

Putting everything together

We have built a lot of infrastructure, but we have never seen exactly how to use it to compute on concrete data.

Reading and writing Z-sets from CSV data

We start by writing two helper functions to read and write positive Z-Sets from CSV (comma-separated values) data. We use serialization facilities from the jackson project. The following two functions read/write POJO (Plain Old Java Objects) from/into CSV strings, including headers:

public static <T> ZSet<T, Integer> fromCSV(String data, Class<T> tclass) {
    try {
        CsvMapper mapper = new CsvMapper();
        CsvSchema schema = CsvSchema.emptySchema().withHeader();
        MappingIterator<T> it = mapper.readerFor(tclass)
                .with(schema)
                .readValues(data);
        List<T> collection = new ArrayList<>();
        it.readAll(collection);
        return new ZSet<>(collection, IntegerWeight.INSTANCE);
    } catch (IOException ex) {
        throw new RuntimeException(ex);
    }
}

public <T> String toCsv(ZSet<T, Integer> data, Class<T> tclass) {
    try {
        Collection<T> values = data.toCollection();
        CsvMapper mapper = new CsvMapper();
        final CsvSchema schema = mapper.schemaFor(tclass).withUseHeader(true);
        ObjectWriter writer = mapper.writer(schema);
        StringWriter str = new StringWriter();
        writer.writeValue(str, values);
        return str.toString();
    } catch (IOException e) {
        throw new RuntimeException(e);
    }
}

If you want to compute on a database of persons you need to define a corresponding Person Java class:

@JsonPropertyOrder({"name", "age"})
public class Person {
    @Nullable
    public String name;
    public int age;

    @SuppressWarnings("unused")
    public Person() {}

    public Person(String name, int age) { ... }

    @Override
    public String toString() { ... }

    @Override
    public boolean equals(Object o) { ... }

    @Override
    public int hashCode() { ... }
}

Remember that Z-sets use HashMaps to store the data, so every value that appears in a Z-set must implement proper equals and hashCode Java methods!

We can easily read Persons from CSV data:

public static ZSet<Person, Integer> getPersons() {
    String data = "name,age\n" +
            "Billy,28\n" +
            "Barbara,36\n" +
            "John,12\n";
    return fromCSV(data, Person.class);
}

Unit tests for Z-set operations

And now we can write a unit test for where:

@Test public void testWhere() {
    ZSet<Person, Integer> input = getPersons();
    ZSet<Person, Integer> adults = input.filter(p -> p.age >= 18);
    ZSet<Person, Integer> expected = fromCSV("name,age\n" +
            "Billy,28\n" +
            "Barbara,36\n", Person.class);
    Assert.assertTrue(expected.equals(adults));
}

We are using a helper function in Z-sets to check that two Z-sets are equal:

public class ZSet<Data, Weight> {
    // extending existing class

    public boolean equals(ZSet<Data, Weight> other) {
        return this.subtract(other).isEmpty();
    }
}

Here are some tests for set operations:

@Test public void testExcept() {
    ZSet<Person, Integer> input = getPersons();
    ZSet<Person, Integer> adults = input.filter(p -> p.age >= 18);
    ZSet<Person, Integer> children = input.except(adults);
    ZSet<Person, Integer> expected = fromCSV("name,age\n" +
            "John,12\n", Person.class);
    Assert.assertTrue(expected.equals(children));
}

@Test public void testUnion() {
    ZSet<Person, Integer> input = getPersons();
    ZSet<Person, Integer> adults = input.filter(p -> p.age >= 18);
    ZSet<Person, Integer> children = input.except(adults);
    ZSet<Person, Integer> all = adults.union(children);
    Assert.assertTrue(input.equals(all));
}

@Test public void testUnionAll() {
    ZSet<Person, Integer> input = getPersons();
    ZSet<Person, Integer> adults = input.filter(p -> p.age >= 18);
    ZSet<Person, Integer> all = input.union_all(adults);
    Integer johnCount = all.getWeight(new Person("John", 12));
    Assert.assertEquals(1, (int)johnCount);
    Integer billyCount = all.getWeight(new Person("Billy", 28));
    Assert.assertEquals(2, (int)billyCount);
    Integer tomCount = all.getWeight(new Person("Tom", 28));
    Assert.assertEquals(0, (int)tomCount);
}

If we want to write a unit test for SELECT we need to define an additional helper class for the results produced:

class Age {
    public final int age;
    ...
}

@Test public void testSelect() {
    ZSet<Person, Integer> input = getPersons();
    ZSet<Age, Integer> ages = input.map(p -> new Age(p.age));
    ZSet<Age, Integer> expected = fromCSV("age\n28\n36\n12\n", Age.class);
    Assert.assertTrue(expected.equals(ages));
}

Testing aggregates

Let's us build four aggregate computations, in increasing order of complexity:

@Test public void testAggregate() {
    ZSet<Person, Integer> input = getPersons();

    AggregateDescription<Integer, Integer, Person, Integer> count =
            new AggregateDescription<>(0, (a, p, w) -> a + w, r -> r);
    Integer personCount = input.aggregate(count);
    Assert.assertEquals(3, (int)personCount);

    AggregateDescription<Integer, Integer, Person, Integer> sum =
            new AggregateDescription<>(
            0, (a, p, w) -> a + p.age * w, r -> r);
    Integer ageSum = input.aggregate(sum);
    Assert.assertEquals(76, (int)ageSum);

    AggregateDescription<Integer, Integer, Person, Integer> max =
            new AggregateDescription<>(
                    0, (a, p, w) -> Math.max(a, p.age), r -> r);
    Integer maxAge = input.aggregate(max);
    Assert.assertEquals(36, (int)maxAge);

    AggregateDescription<Integer, AvgHelper, Person, Integer> avg =
            new AggregateDescription<>(
                    new AvgHelper(0, 0),
                    (a, p, w) -> new AvgHelper(a.count + w, a.sum + p.age * w),
                    r -> r.sum / r.count);
    Integer avgAge = input.aggregate(avg);
    Assert.assertEquals(25, (int)avgAge);
}

Notice how the aggregates use the weight of the records:

• COUNT adds up the weights. Clearly, if an item has a weight of 2 it has to be counted as 2 items.
• SUM multiples each value by its weight. Clearly, adding a value of 5 with a weight of 2 should add 5*2 = 10 to the sum.
• MAX ignores the weights altogether and just computes on the supplied values. Duplicate values do not influence the result of MAX.
• AVG uses a simple helper class AvgHelper (not shown here) to keep both a count and a sum, and then uses the finalize step of the aggregation to perform the division.

And finally, let's write a test for multiply; this test uses another helper class NameAddress:

@Test
public void testMultiply() {
    ZSet<Person, Integer> input = getPersons();
    ZSet<Address, Integer> address = getAddress();
    ZSet<NameAddress, Integer> product = input.multiply(address, (p, a) -> new NameAddress(p.name, a.city));
    System.out.println(product);
    Assert.assertEquals(input.entryCount() * address.entryCount(), product.entryCount());
}

We have printed the value of product using a helper toString() method for Z-sets which we may discuss in a future blog post:

{
    NameAddress{name='Billy', address='Seattle'} => 1,
    NameAddress{name='John', address='New York'} => 1,
    NameAddress{name='John', address='Miami'} => 1,
    NameAddress{name='John', address='San Francisco'} => 1,
    NameAddress{name='Barbara', address='Miami'} => 1,
    NameAddress{name='Billy', address='San Francisco'} => 1,
    NameAddress{name='Billy', address='New York'} => 1,
    NameAddress{name='Barbara', address='Seattle'} => 1,
    NameAddress{name='Billy', address='Miami'} => 1,
    NameAddress{name='Barbara', address='San Francisco'} => 1,
    NameAddress{name='Barbara', address='New York'} => 1,
    NameAddress{name='John', address='Seattle'} => 1
}

Conclusions

In this blog post we have implemented a set of basic SQL computations and shown how they can be performed on data represented as Z-sets. We have started by defining a criterion which tells us when a Z-set computation correctly emulates a database computation. Z-sets are strictly more expressive than traditional database relations or multisets -- for example, Z-sets can describe collections where elements appear a negative number of times. We require our implementations of database computations to be correct for Z-sets that have positive weights.

We have implemented the following operators: SELECT, WHERE, CROSS JOIN, UNION, EXCEPT, and aggregations. A remarkable feature of this implementation is how short the code for each of these operations is: none of the implementations has more than 10 lines of Java. However, let us remember that these implementations are not optimized for performance. However, it is still handy to have a simple implementation around: if we build a more complicated one, optimized for speed or memory, we can compare the behavior with the simple one to more easily find bugs.

In the next blog post in the series we implement additional operations, such as GROUP BY, JOINS, and aggregations on groups.

Footnotes

1. Mathematicians call such diagrams "commutative diagrams": no matter which path you take from a source to a sink in this diagram, you should obtain the same result.
2. SQL is very peculiar in this respect: for some functions like COUNT(*) the result for an empty collection is 0, but for functions like COUNT() or SUM the result is NULL for a collection which has only NULL values; doing this properly will require some additional machinery. We have not discussed at all how to implement NULL values, so far all our Z-set operations work with an abstract Data type; we will discuss NULLs in a future blog post. Here we build an implementation which returns 0 for an empty set.)