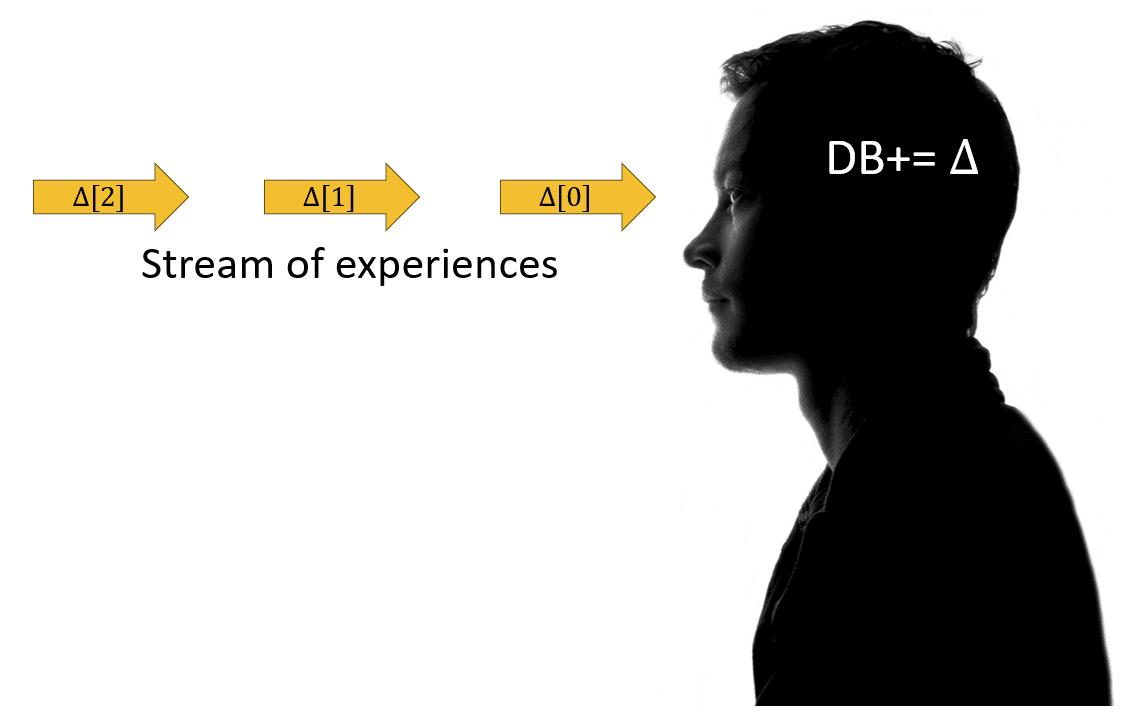
Stream integration

In this blog post we informally introduce one of the core streaming operations in DBSP (our underlying theory of incremental computation): integration.

Integration sounds scary, and if you never liked calculus you may be intimidated. But don’t worry, the integrals in this text are simple, and if you have written even simple computer programs you have already built integrals yourself.

A simple example

Consider the following Java code fragment:

int sum(int[] data) {
 int sum = 0;
 for (int i = 0; i < data.length; i++) {
   int d = data[i];
   sum = sum + d;
 }
 return sum;
}

Any beginner programmer can tell you that this program adds up the values in an array data of integer values. sum is the integral of the values in data. That’s all: an integral is essentially a sum.

The first time I saw such a program I was a little confused by the statement sum = sum + d. To mathematicians this looks like an equation with no solutions (unless d is zero). All programming languages inspired by FORTRAN use = to indicate assignment and not equality. In languages from the C family the test for equality is written as ==.

This is actually a rather unfortunate choice, since mathematicians have been using = for equality for much longer than programmers. Languages such as Pascal had a different symbol for assignment: :=. The fact that = is an expression that returns a value is even worse; there was even an old joke about this:

The last “C++” bug has been identified by a world-wide consortium of computer scientists:

if (nuclear_war = true)
   launch_missiles();

One interesting thing about the statement sum = sum + d is that sum is used in two different ways:

in the right hand side of the assignment, sum refers to the current value of the sum variable.
in the left hand side of the assignment sum refers to the next value of the sum variable.

As we know, programs execute in steps; the execution of the assignment first reads the current value of the variable sum, uses it to add the current value of d, and finally overwrites the value of sum with the result of this computation.

(In a future blog post we will see that in DBSP this ambiguity about the “current” and “next” value of sum is solved cleanly by having an explicit operator, called “delay”, to access the prior value.)

Note that the value of sum may go up or down as values are added, depending on whether data contains positive or negative values.

You can think of the value of sum as being a sequence of different values evolving in time. We can make this more apparent by rewriting the previous program in a different way:

int sum2(int[] data) {
 int[] sum = new int[data.length + 1];
 sum[0] = 0;
 for (int i = 0; i < data.length; i++) {
   sum[i + 1] = sum[i] + data[i];
 }
 return sum[data.length];
}

This is not very efficient, because it uses a different variable sum[i] for each new result computed. But it makes explicit the way the sum evolves in time; each element of the sum array is assigned only once.

The value of sum array computed by this function is also called the prefix sum of the array data.

Integrals in SQL

The SUM aggregate function in SQL can be used for integration: given a collection of values, it will compute the sum of the values. Here is an example which sums up all values in column x of table t:

SELECT SUM(x) FROM t

In SQL SUM is an instance of an aggregate function. Aggregates are really generalizations of integrals.

Your bank account is a stream integrator

Consider your bank account. How does it work? Every time you make a deposit, the saved amount grows. Every time you make a withdrawal, the saved amount shrinks. At any time the total savings in your bank account are exactly the integral of all the deposits you have performed (where withdrawals are deposits with negative amounts). Your bank may have some mechanisms in place which prevent the total amount from becoming negative. But this does not change the fundamental nature of your account as functioning as integrator – it just precludes some operations from being made.

Your refrigerator is a stream integrator

How does your refrigerator work? You buy stuff, and you put it inside. When you want to eat something, you take it out. The content of the refrigerator at any time is nothing but the integral of all the things you have inserted (where removing something counts as an insertion with a negative sign). So your refrigerator is also an integrating device. Like your bank account, it also has built-in overdraft protection: you cannot eat something you haven’t previously inserted.

Databases are stream integrators

So far we have seen examples where integration operates on numbers. But we can find even more interesting examples by generalizing the notion of “addition”.

How do databases work? Let’s first assume that we have a database with a single table to keep things simple. When you initially created the table, it started out empty. But in the course of time you have added and deleted rows in this table. What is the content of the table today? If you think of each insertion as a positive value, and of each deletion as a negative value, then the table’s contents is really nothing but the integral of all the data that has been added to the table!

A standard database also has built-in “overdraft protection”: it won’t let you delete values from a table which aren’t already there.

This view works even better if you model each database table as a Z-set Z-sets: a collections where elements can have positive or negative weights. Then insertion and deletion are both additions, with positive and negative weights. Let’s see how it works using a concrete implementation in the next section.

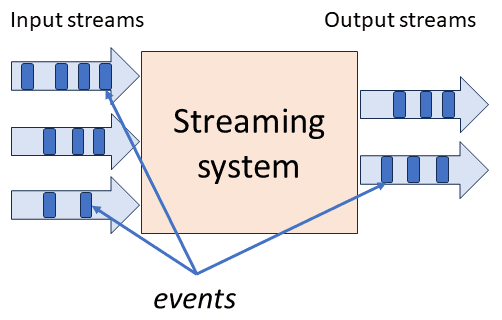
Integration as a streaming operator

Integration is a very useful operation in the context of streaming computations. Both inputs and outputs of a streaming operators are streams – sequences of data values. In our implementation for each stream we only need to remember the “current” value. We also assume that the values in streams are collections (e.g., Z-sets):

public class Stream {
 final CollectionType dataType;
 @Nullable
 BaseCollection currentValue;

 Stream(CollectionType dataType) {
   this.dataType = dataType;
   this.currentValue = null;
 }

 public void setValue(BaseCollection value) {
   this.currentValue = value;
 }

 public BaseCollection getCurrentValue() {
   assert this.currentValue != null;
   return this.currentValue;
 }
}

(The full java code is available in the Feldera repository under the directory sql-to-dbsp-compiler/simulator)

A synchronous operator waits for an input (or multiple inputs for operators such as “join”), does some processing, and then it produces a corresponding output before accepting a new input. We will dedicate another blog post to a detailed description of how streaming operators work, but here an implementation sketch:

/** Base class for operators */
public abstract class BaseOperator {
 final Stream[] inputs;
 final Stream output;

 protected BaseOperator(CollectionType outputType, Stream... inputs) {
   this.inputs = inputs;
   this.output = new Stream(outputType);
 }

 /** Execute one computation step: gather data from the inputs,
 * and compute the current output. */
 public abstract void step();

 /** Initialize the operator.  By default it does nothing. */
 public void reset() {}
}

/** Operator with one single input */
public abstract class UnaryOperator extends BaseOperator {
 UnaryOperator(CollectionType outputType, Stream input) {
   super(outputType, input);
 }

 public Stream input() {
   return this.inputs[0];
 }
}

There are two kinds of streaming operators: stateless, and stateful. A stateless operator remembers nothing from an input to the next; each output is just a function of the current input.

Here is a stateless operator which can be used to implement the functionality of SQL SELECT statements:

/** Apply a function to every element of an input collection to produce the output collection */
public class SelectOperator extends UnaryOperator {
 final RuntimeFunction<DynamicSqlValue, DynamicSqlValue> tupleTransform;

 public SelectOperator(CollectionType outputType,
 RuntimeFunction<DynamicSqlValue, DynamicSqlValue> tupleTransform,
 Stream input) {
   super(outputType, input);
   this.tupleTransform = tupleTransform;
 }

 @Override
 public void step() {
   ZSet<DynamicSqlValue> input = (ZSet<DynamicSqlValue>) this.input().getCurrentValue();
   ZSet<DynamicSqlValue> result = input.map(this.tupleTransform.getFunction());
   this.output.setValue(result);
 }
}

A stateful operator, in contrast, builds and stores a data structure, which can be updated for each new input received, and which can be used to compute the current output.

(We will see in another blog post that in DBSP the delay operator is the only stateful operator, which remembers just the last value it has received.)

We can easily build an integration operator; clearly, this must be a stateful operator, since the current output depends not only on the current input, but also on all the previous values of the input received. In DBSP the integration operator can be built from two other operators, but for now here is a direct implementation:

public class IntegrateOperator extends UnaryOperator {
 BaseCollection current;

 public IntegrateOperator(Stream input) {
   super(input.getType(), input);
   this.reset();
 }

 @Override
 public void reset() {
   this.current = this.getOutputType().zero();
 }

 @Override
 public void step() {
   BaseCollection input = this.input().getCurrentValue();
   this.current.append(input);
   this.output.setValue(this.current);
 }
}

Notice that on start reset the operator needs to initialize its state to an empty collection (the zero function of the result type). The append operation of the collection is used to add the new input value to the current value.

People as stream integrators

Let us consider one more example: yourself! Consider the stream of information that reaches you through your senses: for example, the stream of words that you are reading in this document using your eyes. What happens to these words? You accumulate them in your brain, one by one, reconstructing the phrases I have written. Then you process these phrases, and the information they convey, and you add the new knowledge to your memories. Your brain is essentially an integrating device!

In fact, we can generalize this claim: all living creatures are stream-integrating devices (in more ways than one); their integration capability is the essential mechanism which allows them to interact with the surrounding world. Not only their brains, but their digestive systems are stream processing devices as well.

Integration and incremental computation

One important feature that makes integration such a useful mechanism is its incremental nature: the knowledge in your brain is built piece, by piece, by modifying the existing structures as you learn more stuff. Incremental updates are efficient under the assumption that the + operation, which appends new knowledge, is efficient.

There exists also a reverse process of forgetting, but we will ignore it in this article, although in a future blog post we will show that it can be a very useful model for a process of garbage-collecting state that is no longer useful!

The incremental learning process of humans can be contrasted with the current process of building large AI systems, which essentially are trained using a massive batch process. Many AI datacenters use 20 to 50 megawatts of power. A human brain works on 10 watts! The bulk of this difference is due to the incremental nature of the data processing in the human brain. (It is also true that the amount of knowledge stuffed into a large AI model is also much larger than what one single human brain can retain, and that the AI learning process is accelerated; but there are also many capabilities where human brains still surpass AI systems).

The incremental nature of brain learning process makes it possible for humans to share knowledge; you can read a book written 2000 years ago, and thus learn from someone who has long been dead – books are streams of information across time and space.

I speculate that a shortcoming of the incremental nature of the human learning process also makes it is difficult to get rid of deeply seated beliefs. That’s why sometimes you need a clean slate – a new human generation – to forget “incorrect knowledge”: see the geocentric theories of the universe as an example.

Today AI systems do not truly learn after being deployed (they use a context, which is of a different nature than the information ingested). I claim that when we discover how to build truly incremental AI systems, we will experience a significant breakthrough in AI training efficiency – in the same way incremental view maintenance can be dramatically more efficient than query re-execution.

Stream Integration