4 posts tagged with "Incremental Computation"
View All Tags
Incremental Computation, a bad case of déjà vu
8 MAY, 2024
Incremental Computation, a bad case of déjà vu
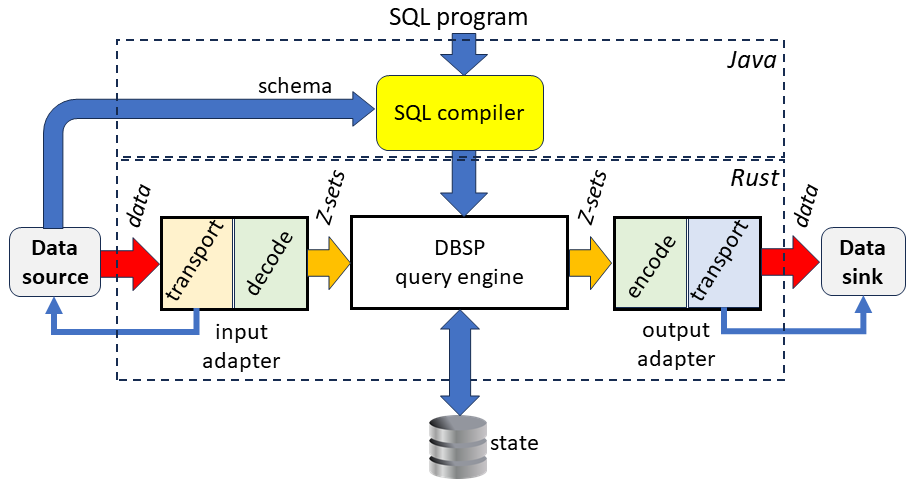
Feldera input and output adapters
16 FEBRUARY, 2024
Interfacing an incremental streaming query engine with the outside world

Incremental Database Computations
1 FEBRUARY, 2024
What is incremental computation in a database

Computing with changes
15 JULY, 2023
Describing how change data and incremental computation work together in Feldera for continuous analytical results.

